Hexagonal binning

binstats(cmd0::String="", arg1=nothing; kwargs...)

Reads arbitrarily located (x,y[,z][,w]) points (2-4 columns) and for each node in the specified grid layout determines which points are within the given radius. These point are then used in the calculation of the specified statistic. The results may be presented as is or may be normalized by the circle area to perhaps give density estimates. Alternatively, select hexagonal tiling instead or a rectangular grid layout.

Parameters

  • C | stats | statistic :: [Type => String | NamedTuple]

    Choose the statistic that will be computed per node based on the points that are within radius distance of the node.

  • I | inc | increment | spacing :: [Type => Str] $Arg = xinc[unit][+e|n][/yinc[unit][+e|n]]]$

    x_inc [and optionally y_inc] is the grid spacing. Optionally, append an increment unit.

  • E | empty :: [Type => Number]

    Set the value assigned to empty nodes [NaN].

  • G | save | outgrid | outfile :: [Type => Str]

    Output grid file name. Note that this is optional and to be used only when saving the result directly on disk. Otherwise, just use the G = gmtbinstats(....) form.

  • N | normalize :: [Type => Bool]

    Normalize the resulting grid values by the area represented by the search_radius.

  • S | search_radius :: [Type => Number]

    Sets the search_radius that determines which data points are considered close to a node. Not compatible with tiling

  • R | region | limits :: [Type => Str or list or GMTgrid|image] $Arg = (xmin,xmax,ymin,ymax)$

    Specify the region of interest. Set to data minimum BoundinBox if not provided.

  • T | tiling | bins :: [Type => String | NamedTuple]

    Instead of circular, possibly overlapping areas, select non-overlapping tiling. Choose between rectangular hexagonal binning.

  • V | verbose :: [Type => Bool or Str] $Arg = [level]$

    Select verbosity level, which will send progress reports to stderr.

  • W | weights :: [Type => Bool | String]

    Input data have a 4th column containing observation point weights.

To see the full documentation type: $@? gmtbinstats$

Binhex

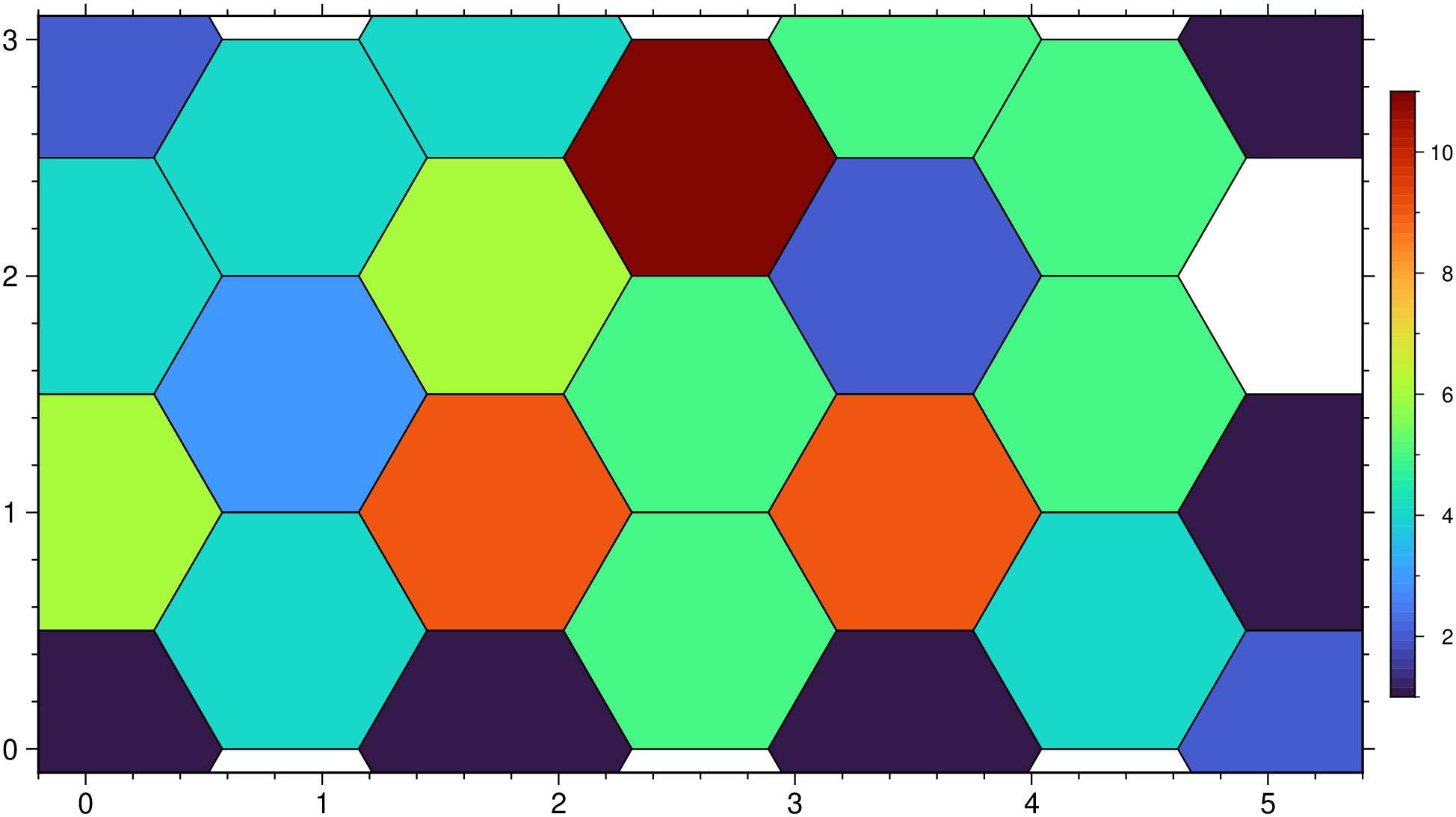
To do hexagonal binning of a random data and counting the number of points inside each hexagon, try:

using GMT
xy = rand(100,2) .* [5 3];
D = binstats(xy, region=(0,5,0,3), inc=1, tiling=:hex, stats=:number);
imshow(D, hexbin=true, ml=0.5, colorbar=true)

© GMT.jl. Last modified: June 07, 2023. Website built with Franklin.jl and the Julia programming language.

These docs were autogenerated using GMT: v1.23.0